Today’s paper: Rethinking ‘Batch’ in BatchNorm by Wu & Johnson

BatchNorm is a critical building block in modern convolutional neural networks. Its unique property of operating on “batches” instead of individual samples introduces significantly different behaviors from most other operations in deep learning. As a result, it leads to many hidden caveats that can negatively impact model’s performance in subtle ways.

This is a citation from the paper’s abstract and the emphasis is mine which caught my attention. Let’s explore these subtle ways which can negatively impact your model’s performance! The paper of Wu & Johnson can be found on arxiv.

The basic idea of the paper is this: most architectures in deep learning today are using BatchNorm layers as they have been shown to lead to much faster training convergence while boosting the performance (e.g. original BatchNorm paper). Unless other layers, BatchNorm operates on the whole batch rather than on individual samples. It’s not so intuitive what effects this can have, so they investigate this in depth.

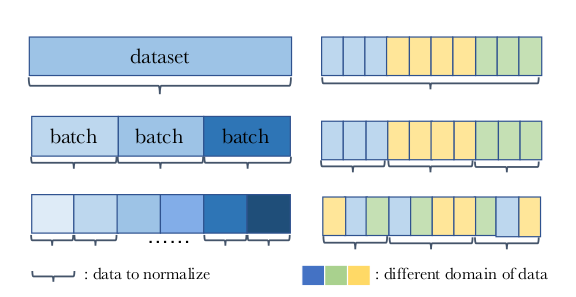
Overall, BatchNorm not only depends on the individual samples, but also on how they are grouped into batches, i.e. the batch size, but also the composition of batches. This can be especially important in medical domains where you might have different sources of data (e.g. different labs).

This is well illustrated in Figure 1 from the paper:

Revisiting BatchNorm

To start off, we will revisit BatchNorm to understand how it’s commonly implemented in deep learning today:

During training, BatchNorm layers keep an exponential moving average of the statistics that are calculated.

The inputs to BatchNorm are CNN features of shape B(atch) x C(hannels) x H(eight) x W(idth). BatchNorm computes the per-channel mean and variance of the data during training and normalizes it. That is: the output of BatchNorm ($y$) is the input minus the mean ($\mu$) divided by the variance ($\sigma²$):

$y = \frac{x - \mu}{\sigma²}$

In this case, $\mu, \sigma² \in R^{C}$.

During training, the exact statistics of the mini-batch can be computed and we denote them with $\mu_{batch}$ and $\sigma²_{batch}$, but during inference we usually don’t have a batch, but rather a single example.

So the goal is to learn the population statistics of the whole training set for the mean and variance for the inference, so ideally we would simply compute this for the whole training set. In practice, this is too expensive on large datasets, so instead, the population statistics are approximated during training by aggregating mini-batch statistics over time usually with an exponential moving average.

To make it clear: at inference time, the BatchNorm layers are frozen to always use the approximated population statistics that were calculated during training.

To stress this further: what is learned during training in the BatchNorm layer is only used during the inference. During training, the BatchNorm layer simply take the exact batch based statistics to normalize the data.

Exponential Moving Average (EMA) to approximate population statistics

So we want to calculate the per-channel means and variances of the training data and we want to approximate it using mini-batches B.

This can be done with the exponential moving average by always taking the linear interpolation of the previous time step and the current time step:

$\mu = \lambda * \mu + (1 - \lambda) * \mu_{batch}$

$\sigma² = \lambda * \sigma² + (1 - \lambda) * \sigma²_{batch}$

where $\mu_{batch}$ and $\sigma²_{batch}$ are the values calculated based on the current mini-batch and $\lambda$ is the momentum parameter (usually >= 0.9).

The authors identify two potential pitfalls here:

1. For large $\lambda$ values, the past contributes more than the present which could be a problem as the model gets constantly updated by gradient descent, but the BatchNorm contribution is largest from the past.

2. For small $\lambda$ values, the EMA becomes dominated by the most recent mini-batches, so likely is not representative of the population.

Alternative to EMA: PreciseBN

The authors suggest to use an alternative to EMA which they name PreciseBN and which apparently was also proposed by the original BatchNorm paper, but most implementations stuck to EMA.

The idea of PreciseBN is to aggregate the statistics over a number of N random samples where N is usually around $10^{3} - 10^{4}$, so a subset of the population, but all evaluated with the same fixed model and not like EMA with constantly changing model parameters during gradient descent.

Identified pitfalls

The paper illustrates several experiments which I won’t cover in detail here, but I want to summarize the lessons learned from those:

• Larger batch sizes suffer more from EMA than smaller batch sizes (here batch sizes 256 vs 8192):
  • The larger the batch size, the noisier the validation error and the worse the overall validation performance
  • However, the final validation error in the end after training for a hundred epochs is not far off (EMA: 24.0, PreciseBN: 23.73)
  • Earlier during training this is very visible and there is a large gap, so this could be more important if you train preliminary sweeps / hyperparameter tuning runs
• Very small batch sizes have trouble computing the statistics properly and the error accumulates in deeper layers

-> It is especially important to consider the effects when evaluating models before they have fully converged, e.g. in reinforcement learning or experiments with small number of epochs trained, e.g. in hyperparameter sweeps.

Moreover, even for converged models, EMA is doing a poor job when using very small batch sizes.

If you have train-test data shifts, then it’s also very important to look at this as then the train data you base the statistics on are different than your test data statistics.

Summary

I really like that the authors dive deep into BatchNorm as it’s used so widely, yet, still not fully understood. The paper has a lot more details and detailed experiments, so it’s definitely worth a read if you considered this blog post interesting.

Overall, the authors show several pitfalls of BatchNorm layers in particular the difference of calculating mini-batch statistics vs estimating population based statistics based off of these mini-batches. One reason for the deviation is the widely used EMA method to calculate the population statistics. Instead, they consider PreciseBN which fares better in experiments especially when training on large batch sizes and when training on only a few epochs.

Another very important area which is covered is gaps in train-test data distributions which often occurs in real life scenarios for example in health data where you train on several labs, but then potentially use the model also on other labs data.